One of the biggest breakthroughts in modern cryptography can have a deep impact in blockchain protocols
Cryptography is at the heart of many blockchain protocols. From traditional proof-of-work(PoW) to L2 modern approaches such as ZK-rollups, many advanced cryptographic methods provide the foundation of blockchain runtimes and protocols.
Consequently, there is an omnipresent question about the security robustness of any blockchain architecture. Naively, we assume that blockchain cryptographic implementations that have survived complex attacks are inherently secured but that’s far from being an empirical proof. Is there a better way to verify the robustness of security algorithms.
The answers seem to be in a new paper that just won the National Security Agency(NSA)’s “Best Cybersecurity Research Paper Competition” causing a lot of noise within the cryptography research community.
Titled “On One-way Functions and Kolmogorov Complexity” the paper provides an answer to one of the quincentennial problems in cryptography.
The problem at hand is related to the existence of a mathematical construct called “one-way functions” that can prove whether a method such as a zero-knowledge proof in an L2 blockchain, is cryptographically secured.
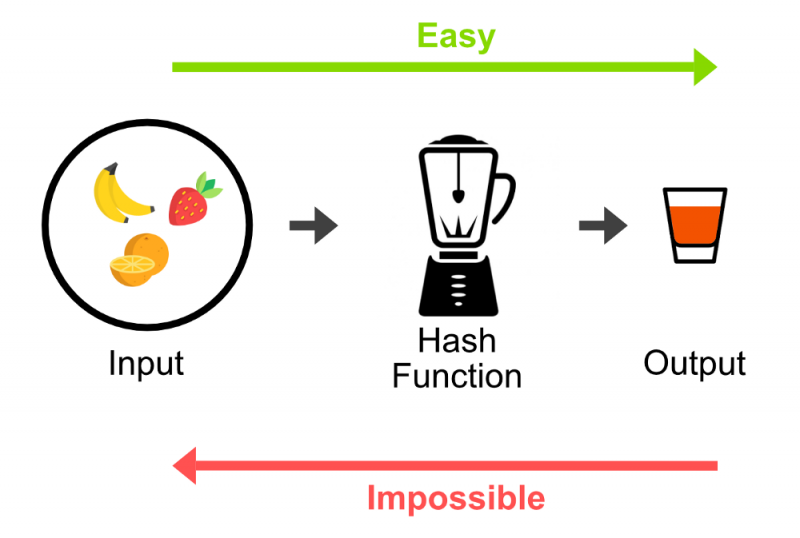
The essence of modern cryptography relies on creating ciphers on data with the hope that they remain secure. However, how can we be sure they are secured?
The theoretical answer to this question came in the 1970s when cryptographers presented the idea of one-way-functions which are mathematical functions that are easy to compute but hard to reverse.
To illustrate how one-way-functions work, think if someone asks you to multiply two large prime numbers like 485144 and 999983.
Arriving to the number 485,135,752,552 as the answer might take some work but we have a method for doing that. Now let’s take the inverse question and start with the number and try to determine its prime factors. That’s a monumentally more difficult task. This is the essence of one-way-functions.
The foundation of cryptographic techniques used in L1 and L2 blockchains is premised on the existence of one-way-functions. If a one-way-function exists for a given problem, then its cryptographically secured and, if not, it’s likely to be vulnerable to different attacks.
However, so far it has been nearly impossible to prove the existence of one-way-functions. In their paper, researchers from Cornell University found an answer drawing parallels to an obscure area of computer science.
Enter Kolmogorov Complexity
The answer proposed in the Cornell research paper essentially states that the existence of one-way-functions is related to another foundational problem of computer science known as Kolmogorov complexity (KC).
The KC theory is related to the complexity of strings of numbers. If you are presented with two large numbers 66666666666666666666 and 123948109102912, you can’t quite prove which is “more random” than the other but intuitively you think the second number is more complex to generate. This was the idea used by Soviet mathematician Andrey Kolmogorov to start a new theory in computational complexity.
Essentially, the KC theory defines the complexity of a number string as length of the shortest possible program that produces the string as an output. Going back to our example, the program required to generate the second number is fundamentally more complex than just printing a sequence of 6s.
KC theory is quite more complex but hopefully you got the core idea. For decades, KC theory has become the foundation of many areas of computer science but hasn’t been that relevant in cryptography. That was until the Cornell research team pull a rabbit out of the hat and showed that the existence of one-way-functions is related to the KC of a given problem. In simple terms, if a problem is KC complex then a one-way-function exists and, if not, likely it doesn’t.
This simple statement might become one of the most revolutionary discoveries in modern cryptography.
What Does that Mean for the Blockchain World?
The Cornell paper provides an empirical way to evaluate the robustness of cryptographic techniques used in L1 and L2 blockchains.
This is particularly relevant considering the emergence of L2 runtimes based on cryptographic techniques such as secure multi party computations or zero knowledge proofs.
Determining whether an algorithm is KC complex is fundamentally simpler than determining the existence of one-way-functions. Granted, this problem expands way beyond the blockchain ecosystem but, if we are talking about building the rails of a new financial system, cryptographic robustness is a foundational capabilities.
Jesus Rodriguez – CEO of IntoTheBlock, Chief Scientist at Invector Labs, I write The Sequence Newsletter, Guest lecturer at Columbia University, Angel Investor, Author, Speaker.
INTERNATIONAL NEWS
Crypto ID promotes international articles about a wide range of topics, including information security, cybersecurity, cryptography, digital identification, encryption, biometrics, blockchain technology, and cryptocurrencies, encompassing data and other technologies related to cybersecurity and digital transformation.
During the last ten years, Crypto ID has been providing innovative content about digital security, identification, and privacy solutions. We celebrate this journey with the certainty that trust is the base for a solid and promising digital future.
Advertising at CRYPTO ID, your organization contributes to the dissemination of technological innovations that enable secure and reliable electronic transactions between businesses and people.
+55 11 3881-0053 | contato@cryptoid.com.br
Você quer acompanhar nosso conteúdo? Então siga nossa página no LinkedIn!
O tema Blockchain tem uma coluna especial no Crypto ID. Acesse aqui e acompanhe tudo relacionado a segurança digital com foco em identificação digital, mobilidade e documentos eletrônicos aplicados a esse universo. Aproveita e dá uma olhada na coluna sobre Criptomoedas, Criptoativos e Tokenização.
